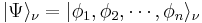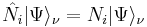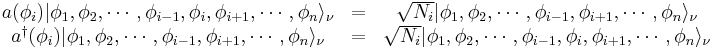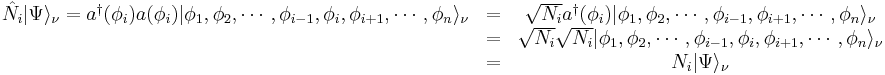Particle number operator

In quantum mechanics, for systems where the total number of particles may not be preserved, the number operator is the observable that counts the number of particles.

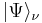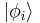The number operator acts on Fock space. Given a Fock state $|\Psi\rangle_\nu$ composed of single-particle basis states $|\phi_i\rangle$ :

$|\Psi\rangle_\nu=|\phi_1,\phi_2,\cdots,\phi_n\rangle_\nu$

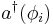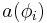with creation and annihilation operators $a^{\dagger}(\phi_i)$ and $a(\phi_i)\,$ we define the number operator 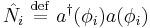$\hat{N_i} \ \stackrel{\mathrm{def}}{=}\ a^{\dagger}(\phi_i)a(\phi_i)$ and we have:

$\hat{N_i}|\Psi\rangle_\nu=N_i|\Psi\rangle_\nu$

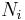where $N_i$ is the number of particles in state 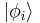$|\phi_i\rangle$ . The above equality can be proven by noting that

$\begin{matrix} a(\phi_i) |\phi_1,\phi_2,\cdots,\phi_{i-1},\phi_i,\phi_{i%2B1},\cdots,\phi_n\rangle_\nu &=& \sqrt{N_i} |\phi_1,\phi_2,\cdots,\phi_{i-1},\phi_{i%2B1},\cdots,\phi_n\rangle_\nu \\ a^{\dagger}(\phi_i) |\phi_1,\phi_2,\cdots,\phi_{i-1},\phi_{i%2B1},\cdots,\phi_n\rangle_\nu &=& \sqrt{N_i} |\phi_1,\phi_2,\cdots,\phi_{i-1},\phi_{i},\phi_{i%2B1},\cdots,\phi_n\rangle_\nu \end{matrix}$

then

$\begin{matrix} \hat{N_i}|\Psi\rangle_\nu = a^{\dagger}(\phi_i)a(\phi_i) |\phi_1,\phi_2,\cdots,\phi_{i-1},\phi_i,\phi_{i%2B1},\cdots,\phi_n\rangle_\nu &=& \sqrt{N_i} a^{\dagger}(\phi_i) |\phi_1,\phi_2,\cdots,\phi_{i-1},\phi_{i%2B1},\cdots,\phi_n\rangle_\nu \\ &=& \sqrt{N_i} \sqrt{N_i} |\phi_1,\phi_2,\cdots,\phi_{i-1},\phi_{i},\phi_{i%2B1},\cdots,\phi_n\rangle_\nu \\&=& N_i|\Psi\rangle_\nu\\ \end{matrix}$

References

Bruus, Henrik, Flensberg, Karsten. (2004). Many-body Quantum Theory in Condensed Matter Physics: An Introduction. Oxford University Press. ISBN 0-19-856633-6.
Second quantization notes by Fradkin

Particle number operator

See also

References